Rolling Motion – It’s a race in SOLIDWORKS MOTION!

Since we are currently in the middle of the high stakes horse racing season here in America, I was inspired to have a virtual race! I am an engineer, so instead of horses, I am going to use SOLIDWORKS Motion to race two solid cylinders down a ramp under the influence of gravity, soap box derby style – go ahead and call me a geek, it is OK. With full rigid body dynamics capabilities including inertia, gravity and solid body contact, Motion can capture the physics involved and reveal the interesting and nonintuitive behavior.

The cylinders are identical in size, but one is made of steel, the other of aluminum. If you were to bet on which is fastest, would you pick the steel or aluminum cylinder?

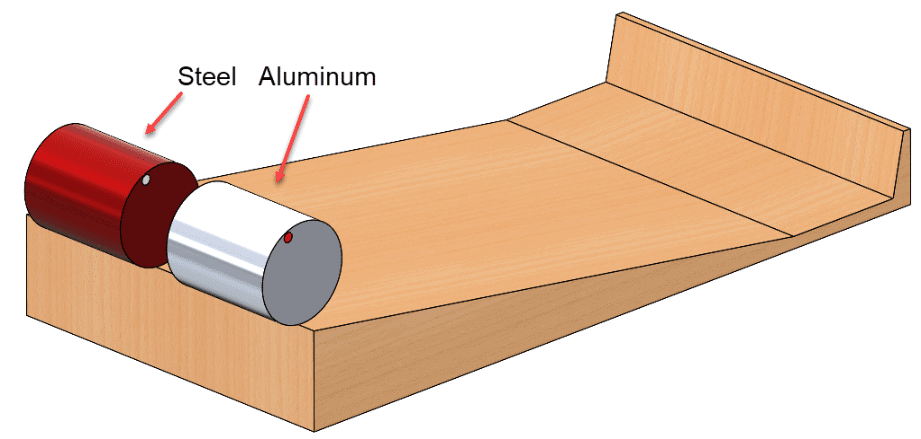
For this idea I credit Walter Lewin, a Dutch astrophysicist and former professor of physics at the Massachusetts Institute of Technology. In a lesson on rolling motion, he very clearly develops the related equations and demonstrates the result of the race described above. His lecture style is brilliant as he uses many simple experiments to help students visualize the physics he is teaching. Many of his recorded lessons are available on YouTube. My favorite is from 2011 about pendulum motion.

If you bet on either cylinder, you would lose the bet. I was informed by my colleague, Bill Reuss, that modern horse races rarely end in a tie, due to the photo-finish camera that can usually distinguish a true winner, but in this race a dead tie would be the result.

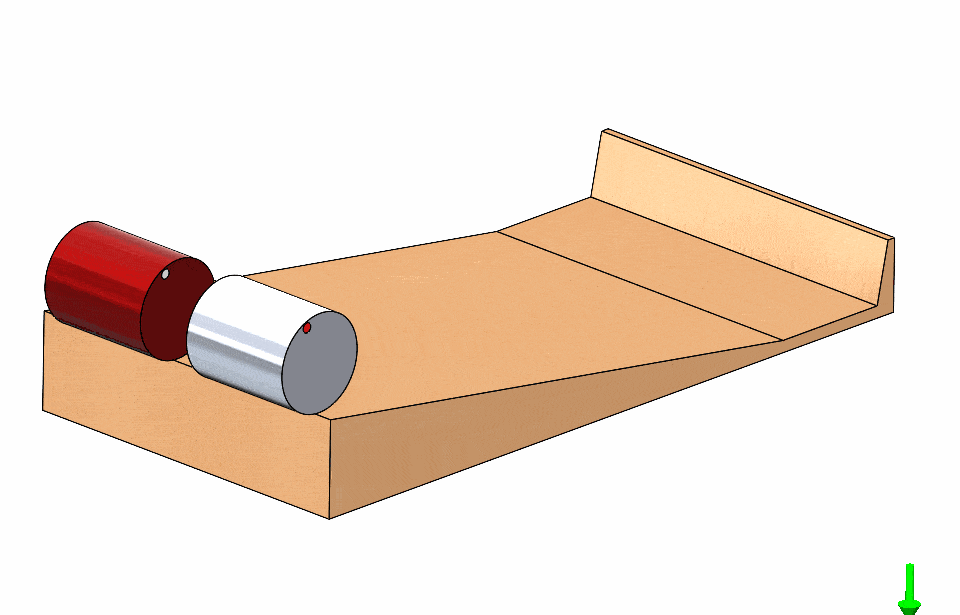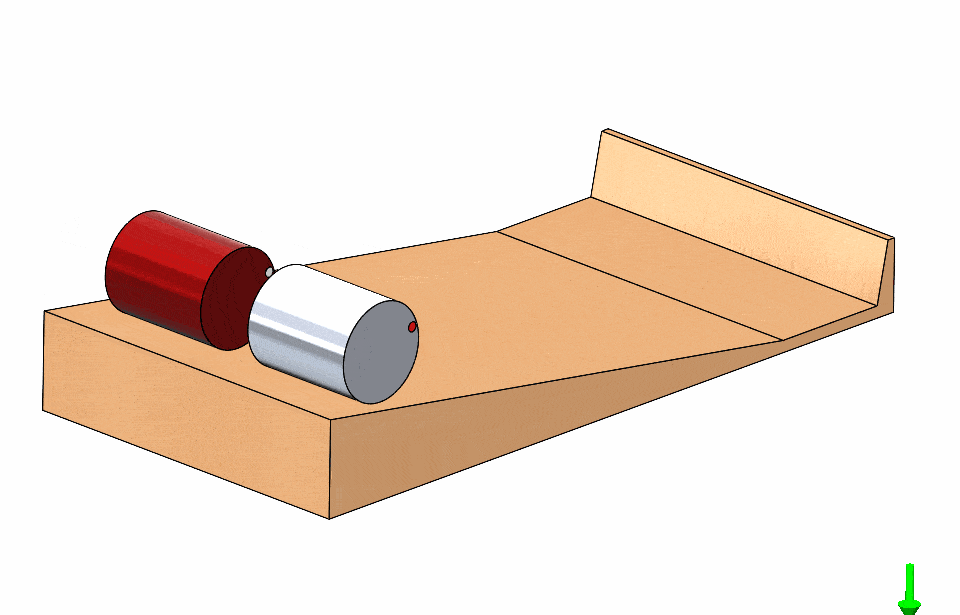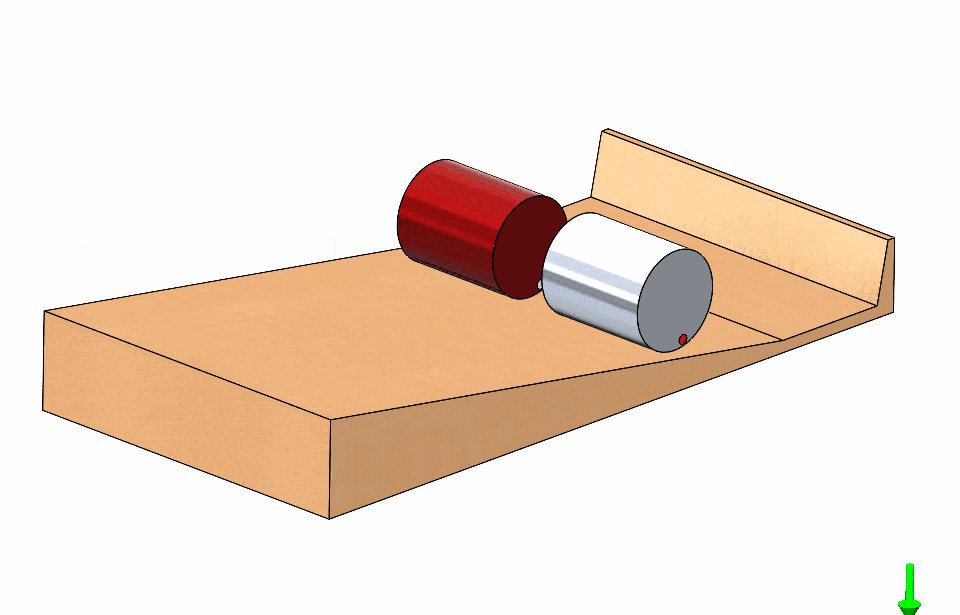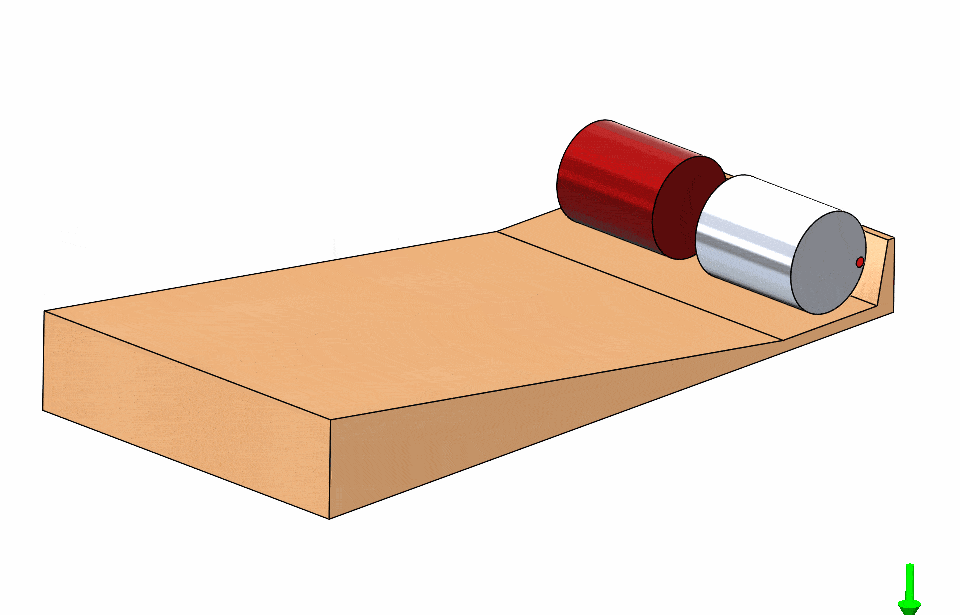
What if you race two cylinders of unequal diameter? Surely one is faster than the other in this situation! Once again, it is a tie!

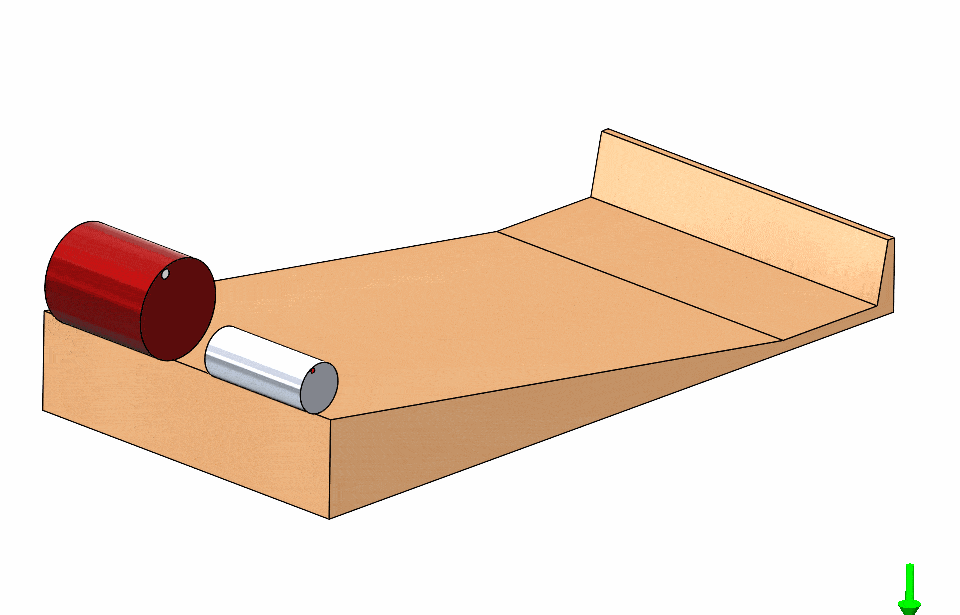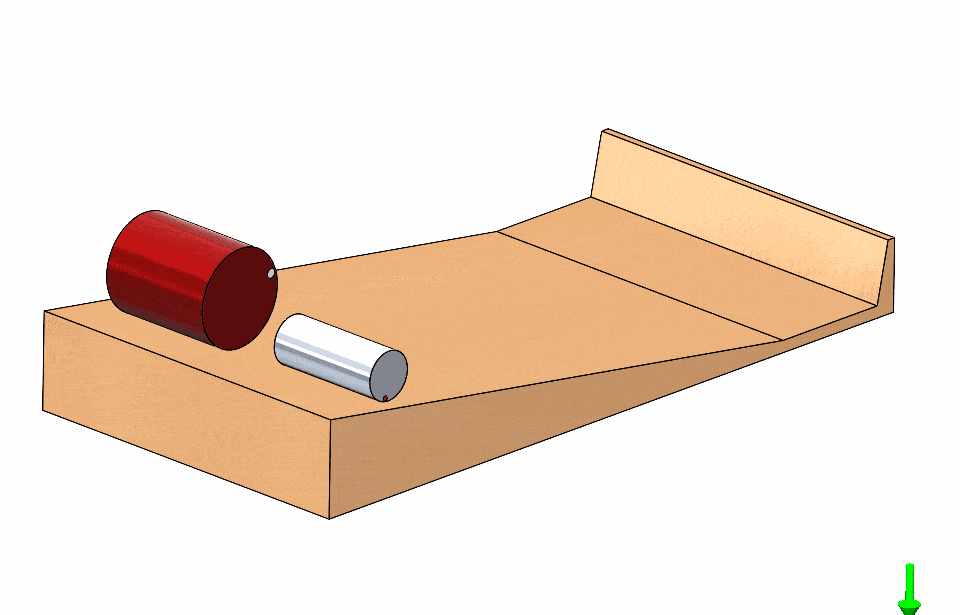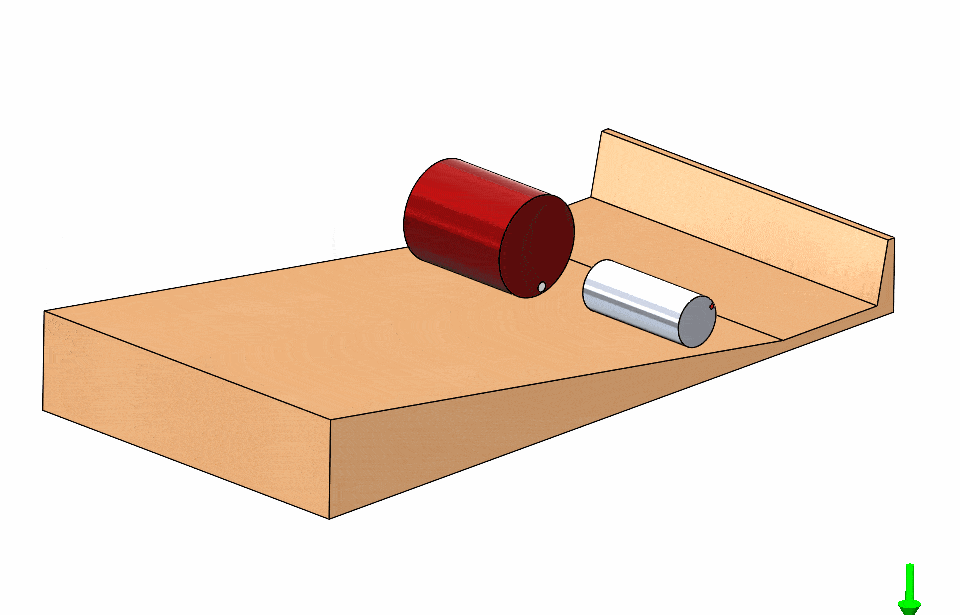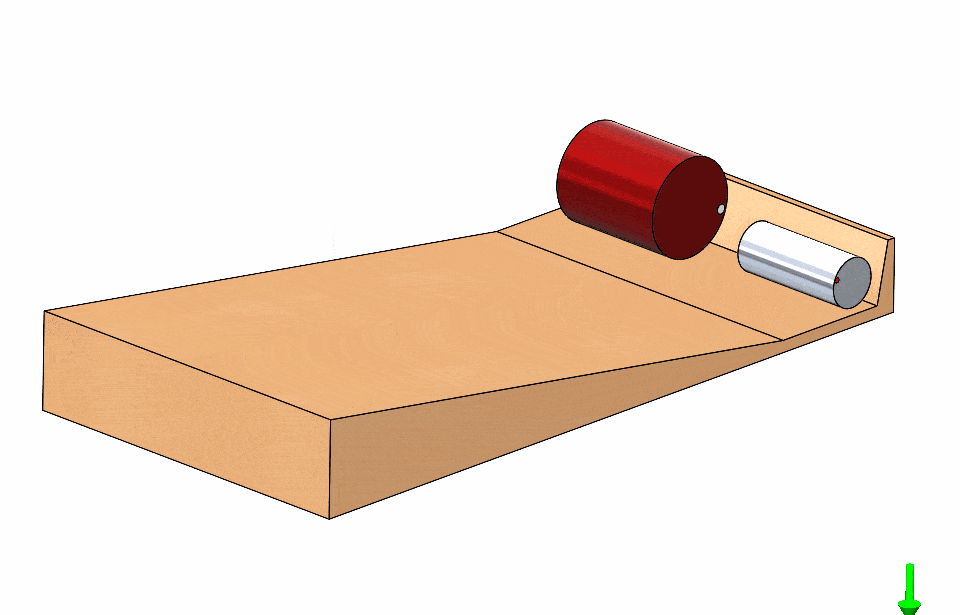
This is very confusing and nonintuitive; is there any condition for which one would be faster? Let us think about the problem at hand. The cylinders start at rest so, if one experiences greater acceleration down the ramp it would clearly be the winner.

Walter Lewin’s recorded lecture on this subject shows the derivation of the equation for acceleration (a) of a cylinder on a ramp for the no-slip (pure roll) condition. View the video if you would like to see the complete derivation. Shown below is the final acceleration equation presented at the 8:44 mark. Here “M” and “R” are cylinder mass and radius, “g” is gravity, “Beta” is the ramp angle, and “I” is the mass moment of inertia of the solid cylinder about its axis.

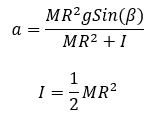
Combining these equations results in the acceleration of a solid cylinder on a ramp of a given angle,

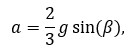
which is only a function of gravity and ramp angle. Surprisingly, it is not related to the mass or radius of the cylinder!

For a hollow (thin-walled) cylinder, as the inner radius approaches the outer radius and the thickness becomes negligible, the moment of inertia is 2X greater than for a solid cylinder:

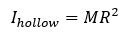
The resulting equation for acceleration of a hollow cylinder is approximately.

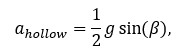
which is about 75% of the acceleration of a solid cylinder. Therefore, the hollow cylinder will always exhibit lower acceleration than the solid cylinder and will always be the slower of the two regardless of size or mass.

Shown below are the results for two additional races of the steel and aluminum cylinders. Both have equal outer diameters; in the first, the aluminum cylinder is hollow, in the second, the steel cylinder is hollow. The solid cylinder always wins.

Solid steel – hollow aluminum:

Solid aluminum – hollow steel:

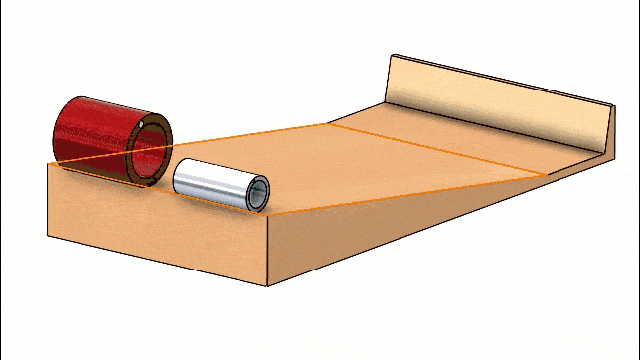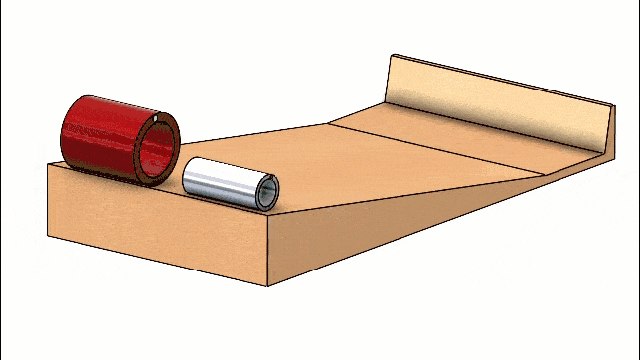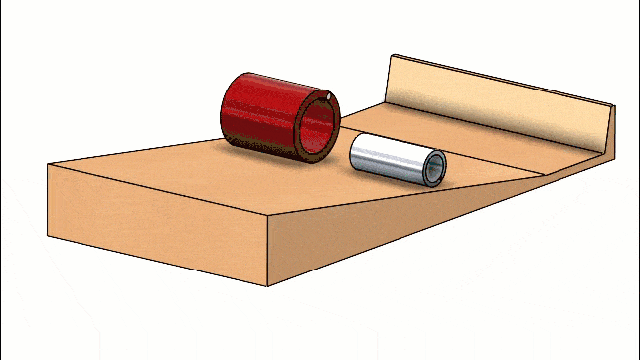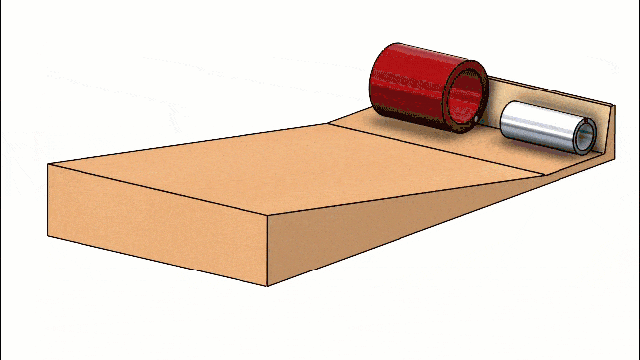
As expected, if both are hollow a tie is the result regardless of the diameter or material.

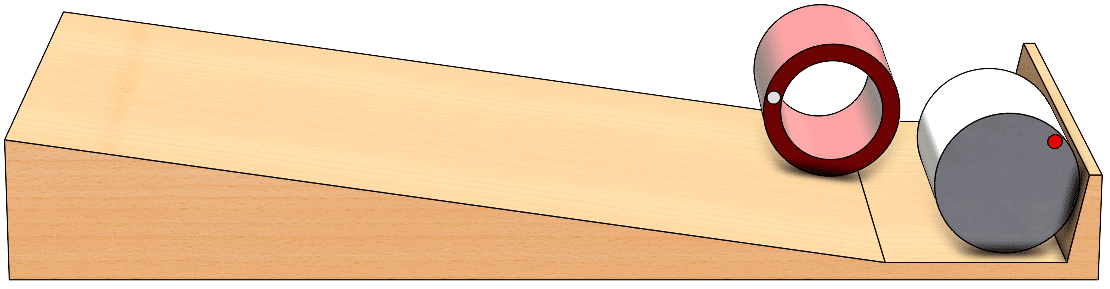
Finally, the same principles apply to spheres. Which of the two shown below are hollow? Both are made of rubber material.

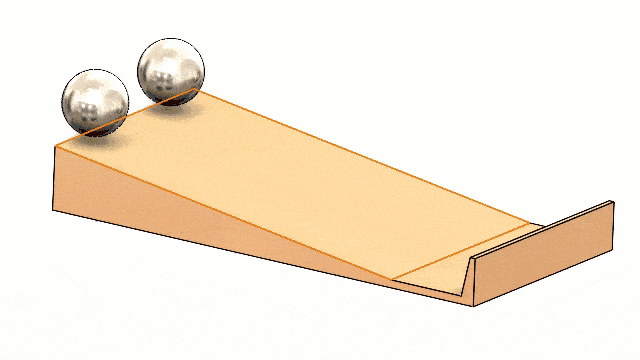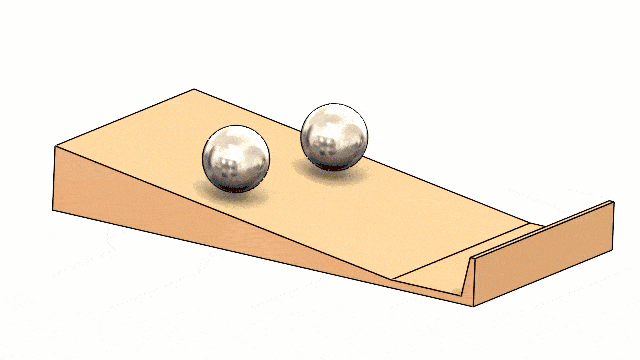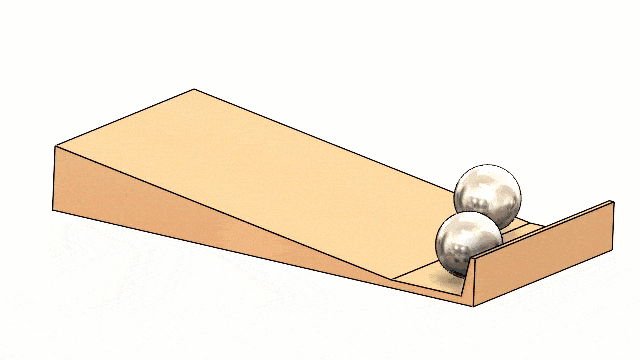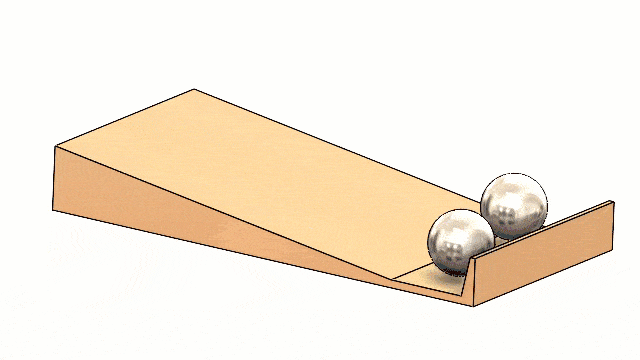
I hope this blog showing how SOLIDWORKS Motion can be used to prove a cool physics concept has been both entertaining and educational! Maybe you can use this information to have some fun with friends and family (or make some cool cash at the bar!) Tell them you learned it from the physics expert, Walter Lewin!

Kurt Kurtin
Sr. Product Manager, Simulation
Computer Aided Technology, Inc.