3 Ways to Control Splines in 3D Space

You’ve got an amazing idea for great swooping loft, sweep, or boundary, but unfortunately using traditional tangency weighting within the feature isn’t working. You’ll need to use a guide curve so a 3D sketch is the best way to go. And since you’re after nice curves, a spline will likely produce the best results.

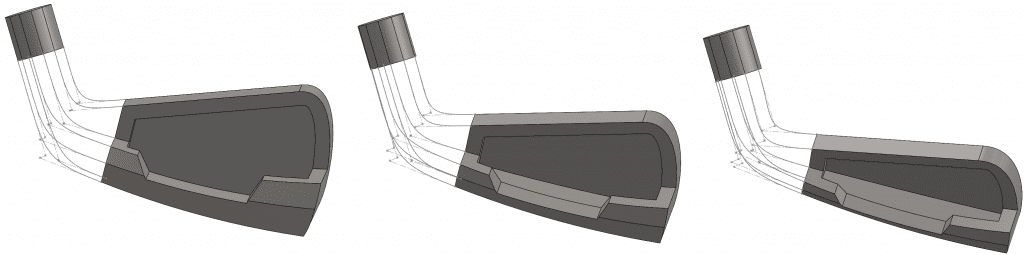
But splines can be tricky to constrain in 2D sketches let alone 3D Sketches. So, let’s take a look at 3 methods for controlling the shape of the spline in 3D Space.

Method 1: Points

The first method you can use to gain control of a spline in 3D Space are points. Points can be added to your 3D sketch and can ‘easily’ have dimensions added to fully constrain them. I intentionally put quote’s around ‘easy’ for dimensioning as you’ll find adding dimensions in 3-dimensional space can be a challenge, so be prepared.

Now I know some readers are going to say, why go through the effort of adding an actual point to the sketch? Can’t we just dimension to spline points? And while you absolutely can dimension to spline points, careful attention must be paid to what happens to the spline by adding an extra control vertex. Remember each vertex on a spline represents a spot on the curve where you want to change curvature. So often times using a control vertex on a spline for the purposes of dimensioning the spline will yield less than desirable results. The easiest way to see this effect is by looking at the Curvature Combs. To activate them Right Click on a Spline and select ‘Show Curvature Combs’

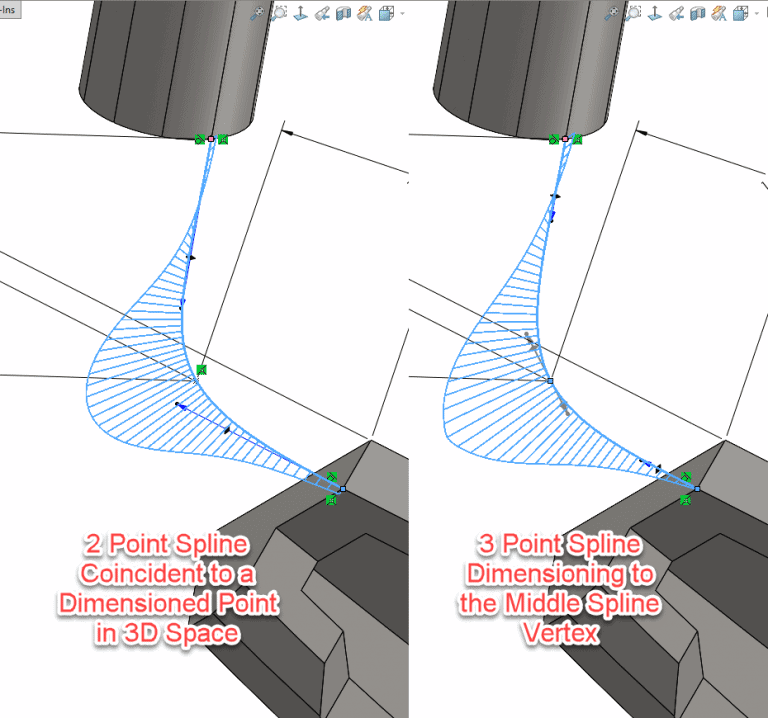
The point method provides nice smooth fully constrained results that can be used for guide curves in subsequent lofts, sweeps, or boundaries. The drawback is that this method often relies on dimensions instead of relations to get the point in a desirable location. As such, updates can be challenging.

Method 2: Fit Spline

The second method you can use to gain control of a spline in 3D space is using a ‘Fit Spline’. To use this method, simply draw lines and arcs that represent the path of your transition. Since lines and arcs are basic geometry, they are much easier to fully define via relationships which can prove to be more robust than a dimensioning style.

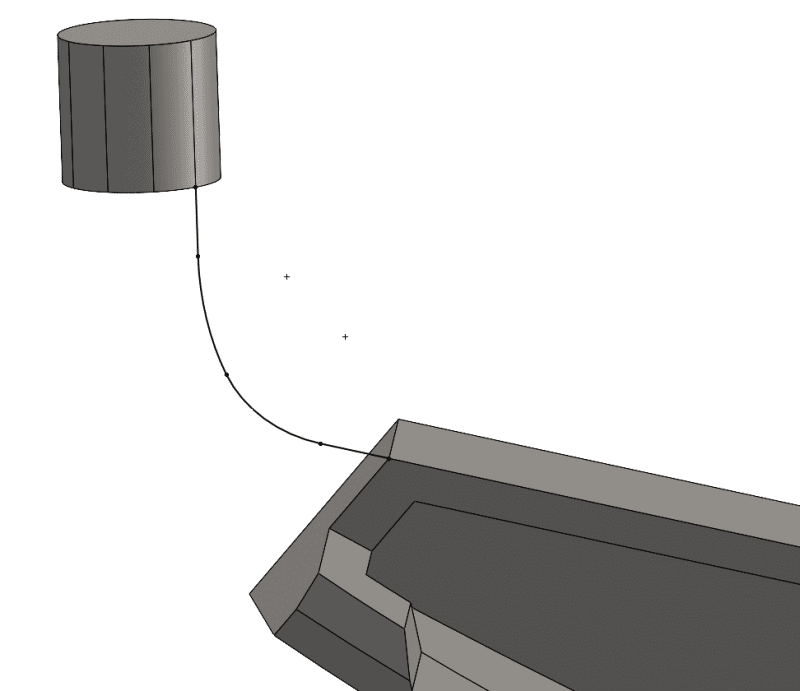
Once the lines and arcs are drawn, select them and use Tools > Spline Tools > Fit Spline. Constraining the spline to the geometry will help allow for consistent updates in the future and often easier use across multiple configurations.

While the fit spline method is easy to obtain consistent results and often does not require dimensions, the resulting curvature of the spline may be less than desirable.

Method 3: Style Spline

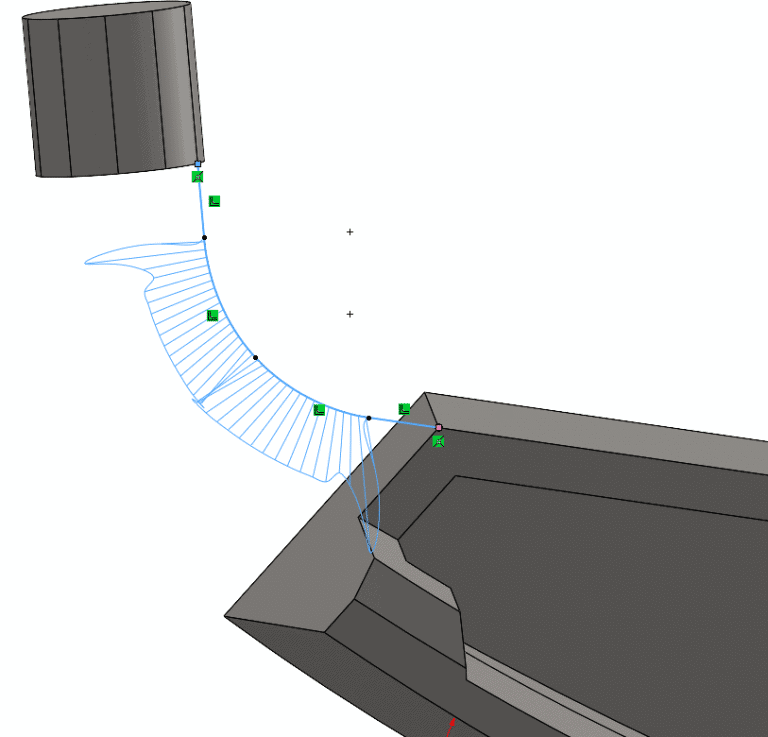
The last method and probably my favorite is the Style Spline. Similar to the fit spline method, the user is required to draw simple geometry (lines) which can be easily defined in 3-dimensional space with either relations or dimensions. To create a Style Spline, select it from the expanded spline menu on the Sketch tab of the Command Manager or use Tools > Sketch Entities > Style Spline.

To draw a style spine, the user is effectively drawing the control polygon of the spline, not the spline itself. As you draw the control polygon, you will notice the lines you draw are construction geometry. From there SOLIDWORKS is interpolating the spline through the drawn control polygon.

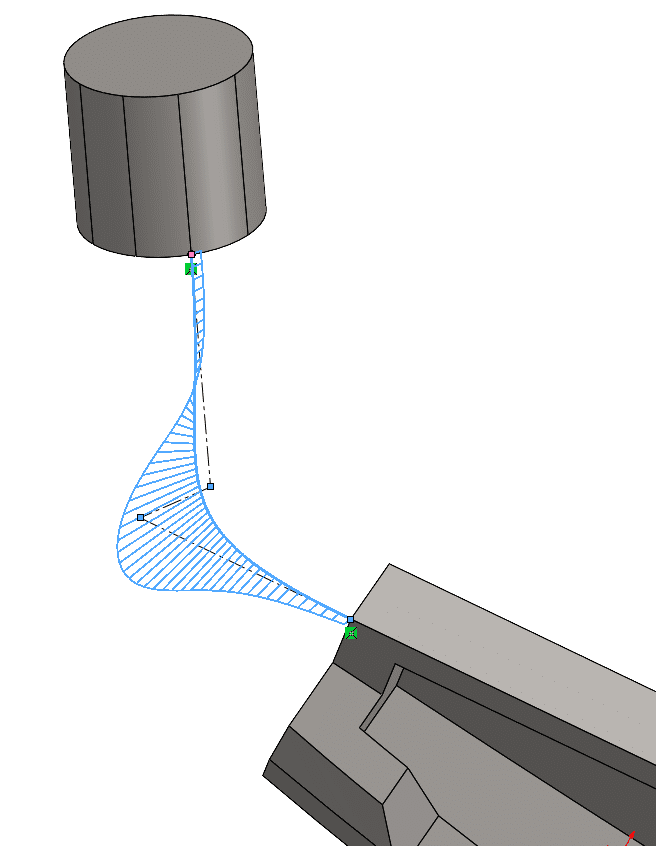
This type of spline is easy to draw, consistent, and easy to constrain in 3-dimensional space. In the example above, co-linear relations have been used with the construction lines and model edges to represent the tangency desired for the transitional segment.

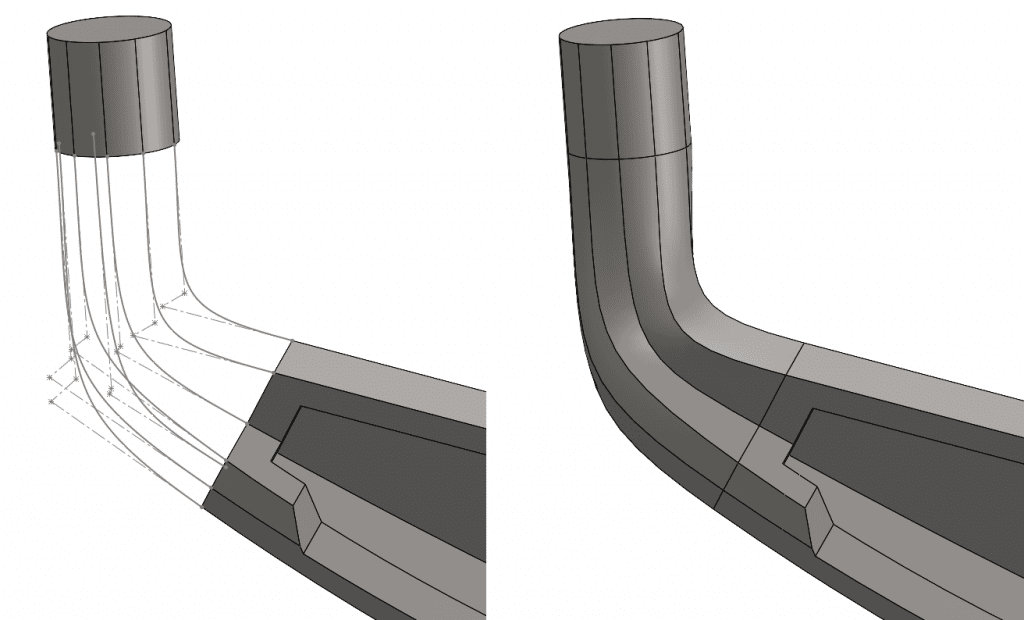
Now multiple 3D sketches can be drawn to help represent the different desired edges to be used during the transition from one solid to the next.

Wrap up

While all the methods listed above are valid, I myself tend to gravitate to the Style Spline when trying to control Splines in 3-dimensional space. The style spline tends to be much easier to control, easier to draw, and more robust when making parametric design modifications. I hope this has been insightful and if you’ve not used a style spline in 3-dimensional space, give it a shot the next time you need to better control a loft, boundary or sweep transitioning along a long complex curve.

Brandon Nelms
Application Engineer Manager
Computer Aided Technology